تجدید ناپذیری منابع معدنی، عدم ­قطعیت داده‌ها و اطلاعات مرتبط، نیاز به سرمایه‌گذاری بالا، طولانی بودن دوره بازگشت سرمایه و غیره، وضعیت خاص و درعین‌حال پرمخاطره‌ای را پیش روی صنعت معدنکاری قرار داده است. ازاین‌رو تلاش شده است با مطالعات و پژوهش­های مختلف، ریسک فعالیت­های معدنی تا حد امکان کاهش یابد. بهینه‌سازی موقعیت گمانه های اکتشافی تکمیلی یکی از مهمترین اقداماتی است که می توان در این راستا انجام داد.

به دلیل محدودیت داده­های برداشت‌شده از رخنمون­های کانسار، برای تهیه اطلاعات بیشتر و کاهش عدم قطعیت تصمیم‌گیری‌ها، اقدام به حفر گمانه ­های اکتشافی می­شود. بر اساس مطالعه نمونه‌های برداشت شده از گمانه­­ها، مدل سه‌بعدی کانسار و به ‌تبع آن مدل بلوکی عیار تخمینی تهیه می‌شود. فرض اساسی در فرآیند برنامه‌ریزی تولید معادن بر این است که این مدل­ها واقعاً ارائه­ گر آن چیزی است که در زمین وجود دارد، حال‌آنکه این مدل‌ها در عمل دارای عدم قطعیت هستند و درنتیجه کلیه طراحی­ های صورت گرفته بر این اساس نیز توأم با عدم قطعیت خواهد بود. راه­ حل کم کردن عدم قطعیت و به‌عبارت‌دیگر افزایش قطعیت، به دست آوردن داده­ های بیشتر از کانسار (گمانه­ های اکتشافی بیشتر) است. نتیجه تعداد بیشتر گمانه ­های اکتشافی، کاهش عدم قطعیت مدل بلوکی و البته افزایش هزینه‌های اکتشافی است. مدل بلوکی با عدم قطعیت کم‌تر، می­تواند برنامه­ های دقیق­ تر و زمان­بندی قابل تحقق­ تری را برای معدن در پی داشته باشد. علاوه بر این، کاهش عدم قطعیت می­تواند در جهت ­گیری استخراج معدن، طرح‌ریزی جریان­های نقدینگی، برنامه­ ریزی دریافت وام برای تأمین مالی پروژه­ ها و حتی در بهره ­برداری از کارخانه فرآوری نیز مؤثر باشد. زمین­ آمار، دانشی است که می­تواند ما را در رسیدن به این هدف یاری نماید.

عدم قطعیت موجود در مدل بلوکی را می‌توان در دو دسته جداگانه تقسیم‌بندی کرد، دسته اول عدم قطعیت موجود در حدود مدل تخمینی (مرزها و محیط پیرامونی کانسار) و دسته دوم عدم قطعیت موجود در داخل کانسار (عدم قطعیت تخمین متغیر در مدل بلوکی).

برای بررسی دقیق و کاهش عدم قطعیت مدل سه راه وجود دارد؛

۱) انجام مطالعات با جزئیات بیشتر (تعداد زیاد گمانه ­های تکمیلی)، ۲) استفاده از اصول زمین‌آماری در مطالعه عدم قطعیت مرزها و تأثیرات آن بر تصمیمات و ۳) استفاده از اصول زمین‌آماری در کنار روش­های بهینه‌سازی تحقیق در عملیات جهت بهینه‌سازی تعداد و موقعیت حفاری‌های تکمیلی.

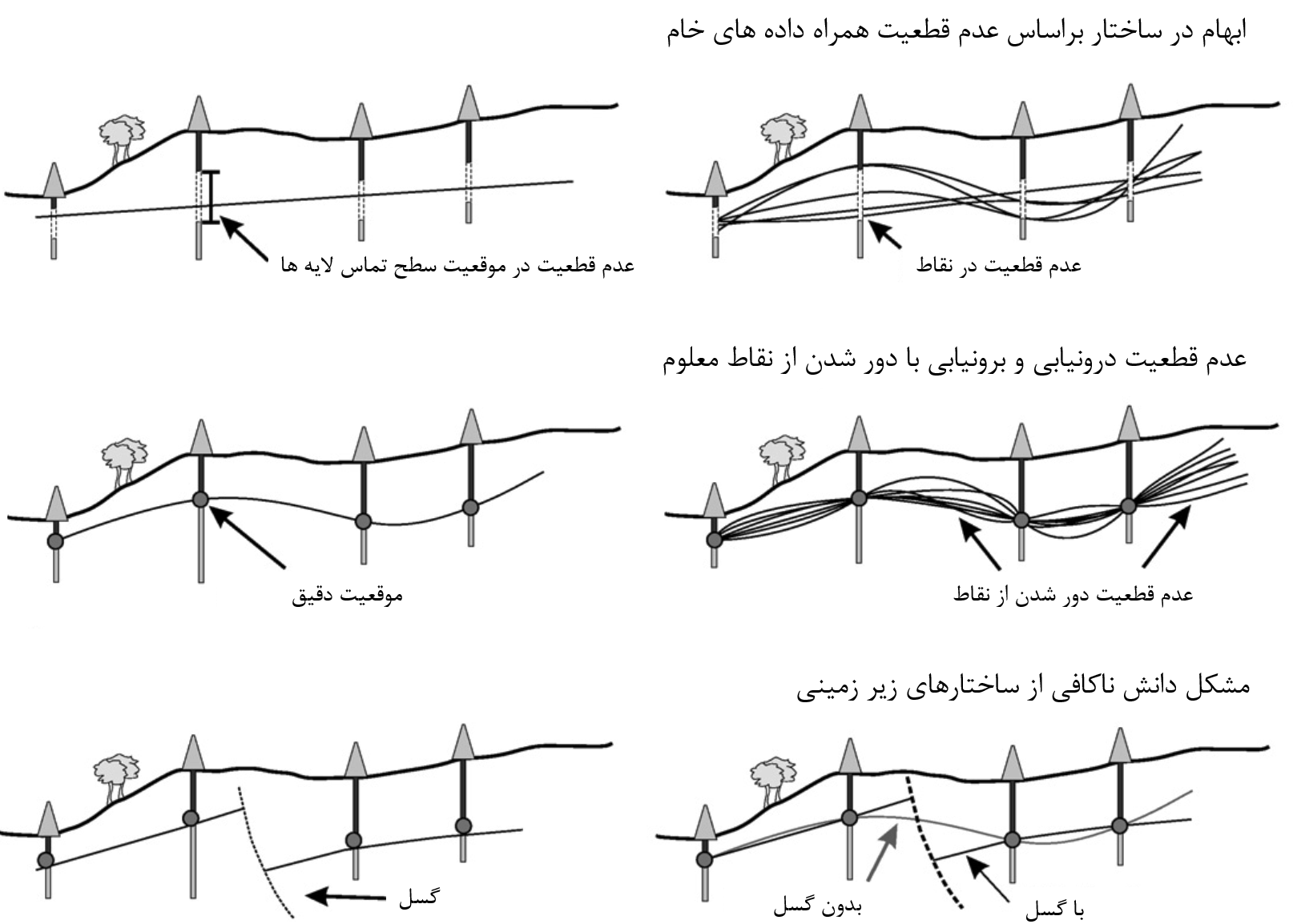
انجام مطالعات با جزئیات بیشتر بسیار هزینه و زمان‌بر است. از طرف دیگر به دلیل ناهمگنی عدم قطعیت در بخش‌های مختلف ذخیره، میزان تأثیر حاصل از افزایش تعداد گمانه‌ها تابعی از مختصات حفر گمانه‌های جدید است (به‌عبارت‌دیگر ارزش اطلاعات به‌دست‌آمده از هر مکانی با مکان دیگر متفاوت است). همچنین محدودیت ­های بودجه ای در پروژه­ های اکتشافی باعث می‌شود تا طراحان در پی کسب بیشترین ارتقا در مدل  از حداقل تعداد گمانه‌های ممکن باشند. به‌عبارت‌دیگر، موقعیت حفر گمانه­ های می­بایست بهینه شود.

 

روش انجام کار

متغیرهای تصمیم

مدل‌های ریاضی شامل سه جزء اصلی هستند: تابع هدف (که باید آن را بهینه نمود)، متغیرهای تصمیم (مجهولات مسئله) و محدودیت‌ها (شرایط محدودکننده مسئله). در پروژه حاضر، متغیر تصمیم شامل موقعیت رأس گمانه‌ها بر اساس طول و عرض جغرافیایی با لحاظ نمودن محدودیت‌های مسئله است.

تابع هدف

یکی از نکات کلیدی در کارایی نتایج حاصل از مسائل بهینه‌سازی، میزان تطابق تابع هدف با نیازی است که بر اساس آن مسئله تعریف‌شده است. تابع هدف متداول در بهینه‌سازی گمانه‌های تکمیلی، کمینه‌سازی واریانس تخمین است. اگرچه کارایی این تابع هدف در شرایطی که هدف از حفر گمانه‌های تکمیلی، بهبود کیفیت تخمین و یا ارتقا رده‌بندی ذخیره است، ثابت‌شده است، اما در مواردی که هدف مطالعه مرزها و تفکیک باطله و ماده معدنی است، با علم به این موضوع که واریانس کریجینگ به تغییرپذیری محلی حساس نیست، استفاده از این تابع هدف مناسب نخواهد بود. در این موارد پیشنهاد می‌شود توابع هدفی متناسب با مسئله و برمبنای معیارهایی همچون خطای رده ­بندی نادرست، واریانس مرکب، واریانس درون‌یابی، آنتروپی اطلاعات، کریجینگ شاخص و احتمال تعریف شود.

فرض­ها و محدودیت­

کانسار موردبررسی به‌صورت تک عنصری، تک جامعه‌ای و همسانگرد و مرزها از نوع نرم در نظر گفته خواهد شد. مهم‌ترین محدودیت مسئله بهینه‌سازی موقعیت گمانه‌های تکمیلی، تعداد گمانه‌های پیشنهادی و حدود تغییرات فضای مطالعه است. در مورد فضای مطالعه می‌توان گفت، حدود تغییرات مرزهای محدوده تحت مطالعه چه در جهت شمالی جنوبی و چه در جهت شرقی غربی، حدود تغییرات مدل بلوکی کانسار خواهد بود. ازنظر عمقی نیز گمانه‌های پیشنهادی تا انتهای پایین‌ترین بلوک در موقعیت پیشنهادی ادامه خواهند یافت.

به‌منظور تعیین تعداد گمانه‌های بهینه موردنیاز جهت حل مسئله نیز می‌توان از برقراری توازن میان تأثیر افزایش تعداد گمانه حفاری تکمیلی بر تغییرات تابع هدف و هزینه حفاری استفاده کرد. بدین‌صورت که مسئله برای تعداد مختلف گمانه‌های تکمیلی حل و با توجه به منحنی‌های مبادله‌ای بین تغییرات تابع هدف و هزینه حفاری به ازای افزایش تعداد گمانه‌های تکمیلی، تعداد بهینه گمانه‌های موردنیاز جهت حل مسئله تعیین می‌شود. روند کاهشی تابع هدف در ازای اضافه شدن تعداد کم گمانه شدید خواهد بود. با علم به این نکته که هرچه تعداد گمانه‌های تکمیلی افزایش یابد، کاهش بیشتری را در تابع هدف مشاهده می­شود، اما از نقطه‌ای خاص (تعداد گمانه بهینه) به بعد، تغییرات تابع هدف چندان زیاد نیست و با در نظر گرفتن روند افزایشی هزینه هنگفت عملیات حفاری، کاهش نه‌چندان محسوس تابع هدف توجیه‌پذیر نیست.

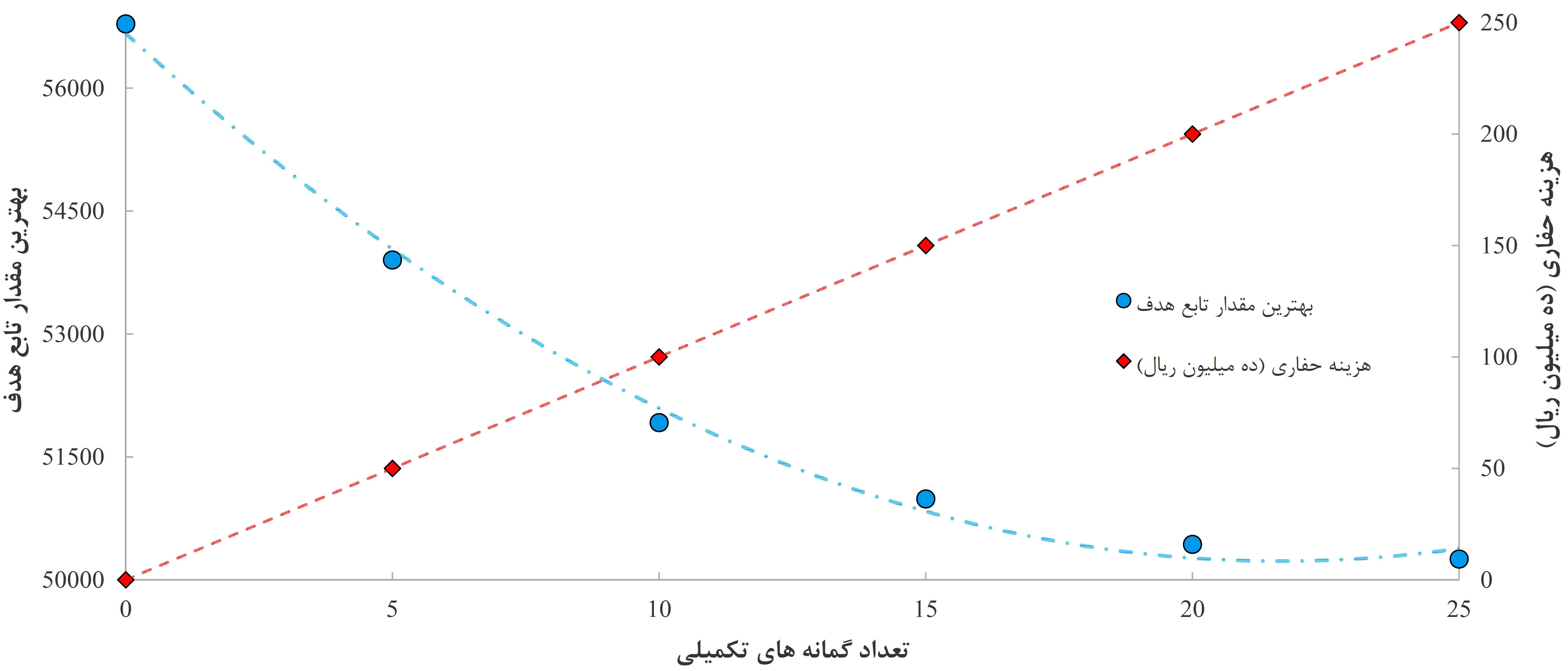
روش­های حل مسئله

در حل مسائلی که تعداد راه‌حل‌های ممکن با بزرگ شدن سایز مسئله و افزایش متغیرها به‌صورت فزاینده‌ای رشد می­کند، استفاده از روش‌های معمول بهینه‌سازی برای پیدا کردن راه‌حل بهینه با توجه به حجم بالای محاسبات، از لحاظ محاسباتی غیرعملی است. روش‌های بهینه‌سازی سنتی با یک کاندیدای واحد شروع شده و با استفاده از یک جستجو تکرارشونده بر اساس یک روش ابتکاری ثابت برای رسیدن راه‌حل بهینه تلاش می‌کنند. در چنین شرایطی استفاده از الگوریتم‌های فراابتکاری که با بررسی تعداد محدودی از حالت‌های ممکن در زمان کوتاه‌تری، به جواب بهینه مسئله نزدیک می‌شوند، مناسب است. در این الگوریتم­ها برخلاف روش­های دقیق بهینه ­سازی، هدف یافتن نقاط تا حد ممکن نزدیک به بهینه سرتاسری هستند، بطوریکه نظر تصمیم­ گیرنده را تا سطح قابل قبولی برآورده سازد. تاکنون روش‌های فراابتکاری فراوانی که عمدتاً بر اساس نظم یا قواعد موجود در ارگانیسم­های طبیعی است ارائه شده‌اند، اما در بین آن‌ها از الگوریتم ژنتیک (GA) ، تبرید شبیه‌سازی‌شده (SA) و ازدحام ذرات (PSO) کاربرد بیشتری گزارش شده است. برای حل مسئله حاضر سه الگوریتم تبرید شبیه‌سازی‌شده، ژنتیک و ازدحام ذرات در نظر گرفته شده‌اند.

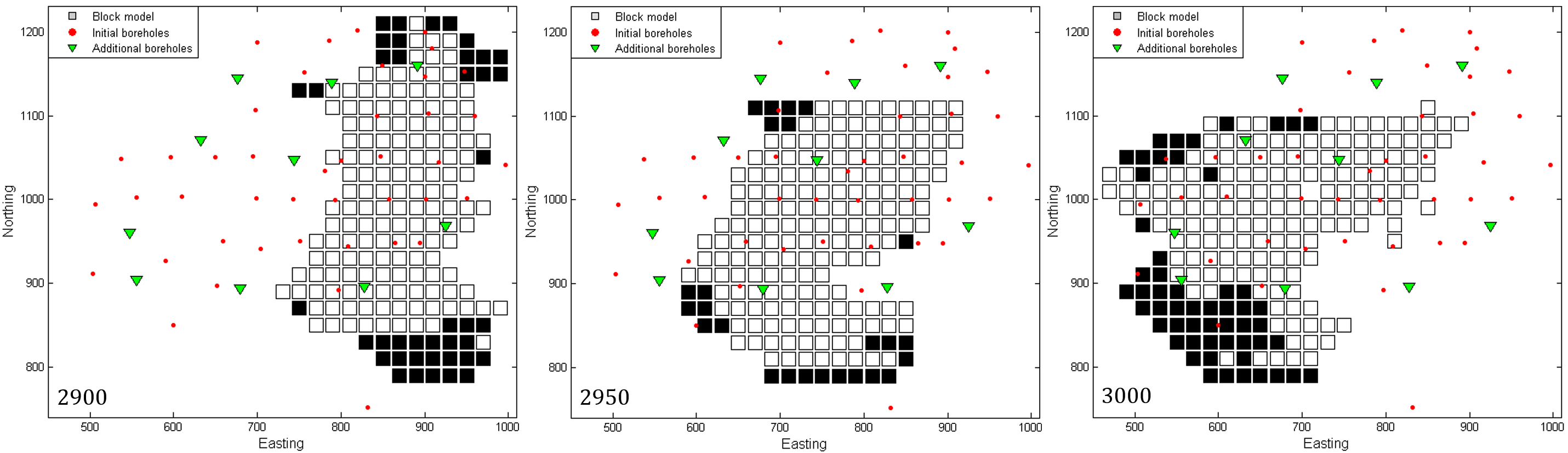
تونایی ما و مزیت استفاده از الگوریتم تیم تخصصی آرکا

آنچه که در عمل در بخش معدن کشور با عنوان بهینه‌سازی موقعیت گمانه‌های اکتشافی انجام می­شود یا به‌صورت انتخاب کارشناس محور است و یا در بهترین حالت، الگوریتم انتخاب موقعیت گمانه­ های جدید از بین تعدادی حالت محدود است و نه یک پروژه بهینه‌سازی!

اما آرکا با همکاری دکتر محمد صفا و دکتر سعید سلطانی محمدی که از معتبرترین و شناخته شده ترین پژوهشگران دنیا در زمینه مکان­یابی گمانه­ های تکمیلی هستند جهت مکان‌یابی از روشی استفاده می­کند که شامل جستجوی موقعیت گمانه­ های جدید در یک محیط سه‌بعدی کاملاً پیوسته و محاسبه مدل بلوکی سه‌بعدی پویا عدم قطعیت مرتبط با الگوی شبکه حفاری پیشنهادی است. نکته مهم و قابل توجه دیگر الگوریتم مورد استفاده توسط تیم آرکا جامعیت آن در مرحله اجرا است. این الگوریتم قابلیت پیاده‌سازی بر روی حجم مختلف داده از معادن بزرگ (چند ده هزار متر حفاری اکتشافی) تا معادن کوچک (چند صد متر حفاری اکتشافی) را داراست.

اهمیت و مزیت استفاده از این الگوریتم زمانی نمود بیشتری خواهد داشت که از منظر هزینه­ های عملیات اکتشاف مورد ارزیابی قرار گیرد. با استفاده از این روش می‌توان حدود ۳۰ تا ۵۰ درصد در هزینه‌های حفاری صرفه‌جویی انجام داد. به‌عنوان نمونه در پروژه حفاری اکتشافی که تعداد ۱۵ گمانه حفاری تکمیلی پیش‌بینی ‌شده است، به راحتی می‌توان با استفاده از الگوریتم تیم آرکا با حدود ۱۰ گمانه جدید همان خروجی را بدست آورد (به عبارتی کاهش تعداد ۵ گمانه). به بیان دیگر تأثیری که ۱۰ گمانه پیشنهادی تیم ما بر روی کاهش عدم قطعیت مدل دارد، مشابه ۱۵ گمانه انتخاب شده توسط کارشناس خواهد بود. با فرض متراژ ۱۰۰ متر برای هر گمانه، و هزینه ۲۰۰ هزار تومان به ازای هر متر حفاری، تنها در عملیات حفاری ۱۰۰ میلیون تومان صرفه‌جویی در هزینه‌های عملیات اکتشاف اعمال خواهد شد. البته در این شرایط هزینه لاگینگ و آنالیز این ۵ گمانه نیز از هزینه­ های عملیات اکتشاف حذف شده است.

برای مطالعات بیشتر در این موضوع میتوانید به منابع ذیل مراجعه نمایید.

Safa, M. and S. Soltani-Mohammadi (2018). “Distance function modeling in optimally locating additional boreholes.” Spatial Statistics 23: 17-35.

Soltani-Mohammadi, S., M. Safa and H. Mokhtari (2016). “Comparison of Particle Swarm Optimization and Simulated Annealing for Locating Additional Boreholes Considering Combined Variance Minimization.” Computers & Geosciences 95: 146-155.

Safa, M., S. Soltani-Mohammadi and M. Kurdi (2016). “Optimal Design of Additional Sampling Pattern for Drinking-Water Quality Control.” Environment, Development and Sustainability: 1-14.

Abbaszadeh, M., A. Hezarkhani and S. Soltani-Mohammadi (2016). “Proposing drilling locations based on the 3D modeling results of fluid inclusion data using the support vector regression method.” Journal of Geochemical Exploration 165: 23-34.

Soltani, S. and M. Safa (2015). “Optimally Locating Additional Drill Holes to Increase the Accuracy of Ore/Waste Classification.” Mining Technology 124(4): 213-221.

Soltani, S. and A. Soltani (2015). “Considering the Epistemic Uncertainties of the Variogram Model in Locating Additional Exploratory Drillholes.” Int. Journal of Mining & Geo-Engineering 49(1): 67-74.

Soltani-Mohammadi, S. and A. Hezarkhani (2013). “Optimum locating of additional drillholes to optimize the statistical value of information.” Journal of Mining and Metallurgy A: Mining 49(1): 21-29.

Soltani-Mohammadi, S. and A. Hezarkhani (2013). “A simulated annealing-based algorithm to locate additional drillholes for maximizing the realistic value of information.” Natural resources research 22(3): 229-237.

Soltani, S. and A. Hezarkhani (2013). “Proposed algorithm for optimization of directional additional exploratory drill holes and computer coding.” Arabian Journal of Geosciences 6(2): 455-462.

Soltani-Mohammadi, S., A. Hezarkhani and A. E. Tercan (2012). “Optimally locating additional drill holes in three dimensions using grade and simulated annealing.” Journal of the Geological Society of India 80(5): 700-706.

Soltani, S. and A. Hezarkhani (2011). “Determination of realistic and statistical value of the information gathered from exploratory drilling.” Natural resources research 20(4): 207-216.

Soltani, S., A. Hezarkhani, A. E. Tercan and B. Karimi (2011). “Use of genetic algorithm in optimally locating additional drill holes.” Journal of Mining Science 47(1): 62-72.

Soltani, S. and A. Hezarkhani (2009). “Additional exploratory boreholes optimization based on three-dimensional model of ore deposit.” Archives of Mining Sciences 54(3): 495-506.